8.Sınıf Önemli Özdeşlikler Konu Anlatımı
- İki Terimin Toplamının Karesi,
- İki Terimin Farkının Karesi ve
- İki Kare Farkı Özdeşliği
konu anlatımı özet ve örnekleriyle konunun anlaşılmasını kolaylaştıracak şekilde tasarlanarak hazırlanmıştır.
| İki Terimin Toplamının Karesi Özdeşliği: |
| İki terimin toplamının parantez karesi, birinci terimin karesi, birinci ve ikinci terimlerin çarpımının iki katı ve ikinci terimin karesinin toplamına eşittir. Kural: ^{^{2}}=a^{2}+2ab+b^{2}) |
örnek: ^{2}) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre)^{^{2}}=x^{2}+2x2+2^{2}&space;=x^{2}+4x+4)
|
örnek: ^{2}) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre)^{^{2}}=(2x)^{2}+2(2x)3+3^{2}&space;=4x^{2}+12x+9)
|
| İki Terimin Farkının Karesi Özdeşliği: |
| İki terimin farkının parantez karesi, birinci terimin karesi, birinci ve ikinci terimlerin çarpımının iki katı ve ikinci terimin karesinin toplamına eşittir. Kural: ^{^{2}}=a^{2}-2ab+b^{2}) |
örnek: ^{2}) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre)^{^{2}}=x^{2}-2x2+2^{2}&space;=x^{2}-4x+4)
|
örnek: ^{2}) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre)^{^{2}}=(2x)^{2}-2(2x)3+3^{2}&space;=4x^{2}-12x+9)
|
| İki Kare Farkı Özdeşliği: |
| İki kare farkı özdeşliği Kural: 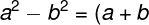.(a-b)) |
örnek: 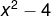 özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre)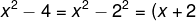.(x-2))
|
örnek: 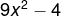 özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre) özdeşliğinin eşitini yazalım.(yukarıdaki kurala göre)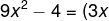^{2}-2^{2}=(3x+2).(3x-2))
|
[ads1]
8.Sınıf Matematik Cebirsel İfadeler konu Anlatımına ait diğer başlıklar için>>
8.Sınıf Matematik Cebirsel İfadelerle ilgili çok test çözmek için>>
8.Sınıf Matematik Cebirsel İfadelerle ilgili Test indirmek için>>
8.Sınıf Matematik daha çok dökümana ulaşmak için>>



