matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi
5.Sınıf Kesirleri Sıralama Konu Anlatımı,güncel müfredata uygun olarak öğrenci odaklı anlamaya yönelik sade bir dille görsellerle desteklenerek anlatılmıştır.
| Kazanım: M.5.1.3.5. Payları veya paydaları eşit kesirleri sıralar. |
| Kesirleri Sıralama |
|
| Örnek: \(\large\frac{4}{7}>\frac{3}{7}>\frac{2}{7}\) |
| Örnek: \(\large\frac{9}{10}>\frac{7}{10}>\frac{5}{10}\) |
| Örnek: \(\large\frac{9}{3}>\frac{7}{3}>\frac{5}{3}\) |
| Örnek: \(\large\frac{6}{6}>\frac{5}{6}>\frac{1}{6}\) |
| Örnek: \(\large2\frac{11}{13}>2\frac{10}{13}>2\frac{7}{13}\) |
| Örnek: \(\large\frac{15}{23}>\frac{13}{23}>\frac{10}{23}>\frac{9}{23}\)> |
|
| Örnek: Aşağıdaki kesirleri büyükten küçüğe doğru sıralayınız. \(\large \frac{1}{2},\frac{2}{3},\frac{5}{6}\) |
|
|
| Örnek: \(\large\frac{1}{3}>\frac{1}{4}>\frac{1}{6}\) |
| Örnek: \(\large\frac{4}{7}>\frac{4}{9}>\frac{4}{10}\) |
| Örnek: \(\large\frac{9}{8}>\frac{9}{9}>\frac{9}{12}\) |
| Örnek: \(\large\frac{11}{14}>\frac{11}{17}>\frac{11}{19}\) |
| Örnek: \(\large2\frac{10}{8}>2\frac{10}{9}>2\frac{10}{13}\) |
| Örnek: \(\large\frac{18}{1}>\frac{18}{2}>\frac{18}{3}\) |
|
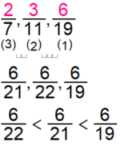
| Örnek: Aşağıdaki kesirleri küçükten büyüğe doğru sırlayınız. \(\large\frac{2}{7},\large\frac{3}{11},\large\frac{6}{19}\) |
Çözümü Göster Çözüm:
|
Tavsiyeler:
- Kesirlerde sıralama soruları testlerde karşınıza geldiği zaman , hangi kuralı kullanacağınızda tereddüt yaşıyorsanız.
- Kesirde payları eşitlemek ,paydaları eşitlemeye göre daha kolaysa paydaları eşitle,
- Kesirde paydaları eşitlemek ,payları eşitlemeye göre daha kolaysa paydaları eşitle.
- Unutma basit kesirler her zaman tam kısımlı kesirden küçüktür.
- Basit kesirler her zaman bileşik kesirlerden küçüktür.
5.Sınıf Kesirleri Sıralama Konu Anlatımı ,sonrasında aşağıdaki sayfaları ziyaret etmenizi tavsiye ediyorum.
5.Sınıf Matematik Test İndirmek İçin>>
5.Sınıf Matematik Konu Anlatımı için>>
5.Sınıf Matematik Testleri Çözmek için>>
5.Sınıf Matematik daha çok içerik için>>
