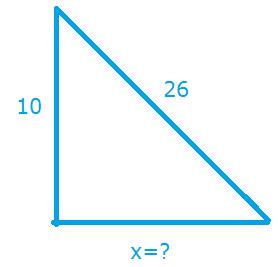matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi
Pisagor (Pythagoras) isimli Yunan matematikçi ve filozoftur.Milattan önce 570 ile 475 yılları arasında yaşamıştır. Dik üçgenin kenar uzunlukları arasındaki ilişkiye ait çalışmalar yapmıştır. Çalışmalar sonunda elde ettiği sonuçlar da Pisagor bağıntısı olarak matematikte yerini almıştır.(wikipedia)
8.Sınıf Pisagor Bağıntısı Konu Anlatımı, önemli hatırlatmalar ve sık karşılaşılan örneklerle konuyu özetler niteliktedir.
| Pisagor Bağıntısı |
| Bir dik üçgende , dik kenarların uzunluklarının kareleri toplamı, hipotenüs uzunluğunun karesine eşittir. |
c kenarı hipotenüs, a ve b dik kenarlardır.
 |
 |
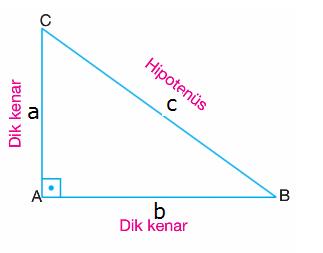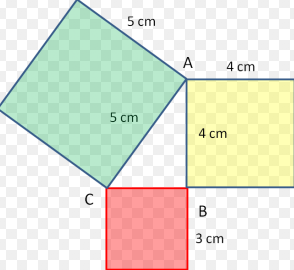| Pisagor kuralının mantığı : Yukarıdaki şekli incelersek dik kenarlara yapışık olan yeşil ve kırmızı karenin alanları toplamı hipotenüse yapışık olan karenin alanına eşittir. |
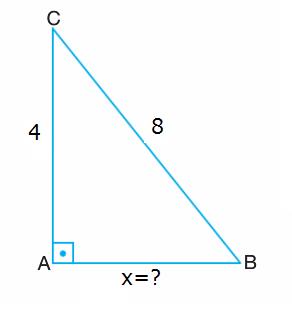
| Örnek:
Çözüm: BC kenarının uzunluğunu x dersek;
olarak bulunur. |
| Örnek:
Çözüm: olarak bulunur |
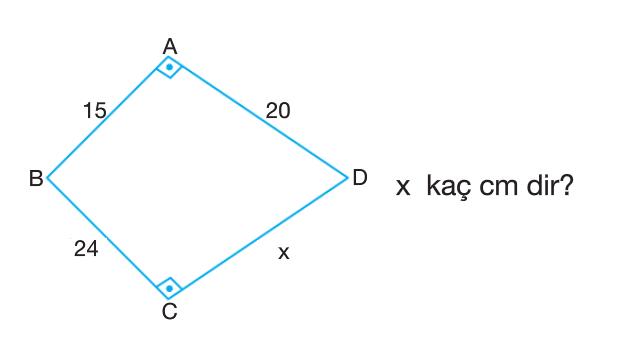
| Örnek:
|
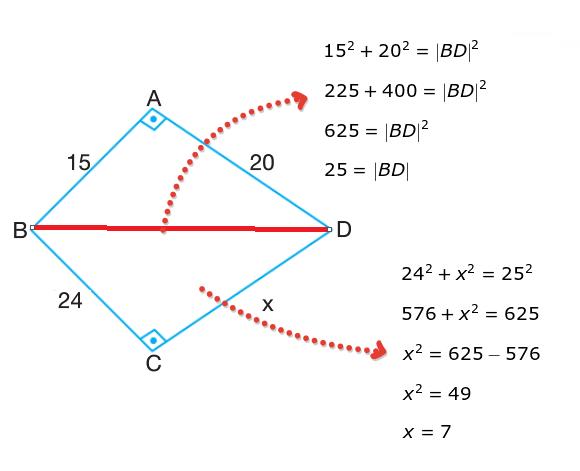
| Çözüm:
|
| ÖZEL ÜÇGENLER |
| 3-4-5 Kuralı |
 |
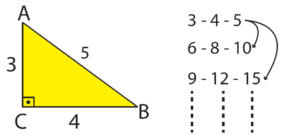Örnek: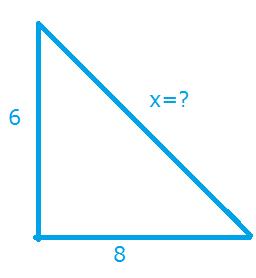 3-4-5 özel üçgen kuralına göre;3 ve 4 ün 2 katı olan : 6 ve 8 bulunduğuna göre hipotenüs de 5.2=10 olarak bulunur. |
| 5-12-13 Kuralı: |
 |
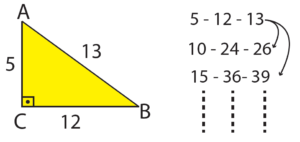| Örnek:
5-12-13 özel üçgen kuralına göre; 5 ve 13 ün 2 katı olan : 10 ve 26 bulunduğuna göre x 12.2=24 olarak bulunur. Diğer kurallar da benzer şekilde kullanılır. |
| 8-15-17 Kuralı: |
 |
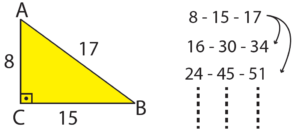| 7-24-25 Kuralı: |
 |
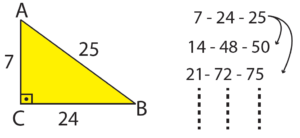8.Sınıf Pisagor Bağıntısı Konu Anlatımı içeriğindeki bilgiler üçgenlerde benzerlik konusunda , eğim konusunda kullanılmaktadır.Bu konudan çok fazlada soru çözmenizi tavsiye ediyorum.
Ayrıca sitemizde Pisagor Bağıntısı ile ilgili tesler mevcuttur.Sitemizde online testler eklenmektedir.İncelemenizi tavsiye ediyorum.
8.Sınıf Matematik Konu Anlatımına ait diğer başlıklar için>>
8.Sınıf Matematik ile ilgili çok test çözmek için>>
8.Sınıf Matematik ile ilgili Test indirmek için>>
8.Sınıf Matematik ile ilgili daha çok dökümana ulaşmak için>>
