8.Sınıf Gerçek Sayılar Konu Anlatımı

8.Sınıf Matematik Gerçek Sayılar Konu Anlatımı Konu Anlatımı güncel müfredata uygun olarak , kitaplardaki popüler soruların benzerleri dikkate alınarak hazırlanmıştır.Konu sonunda linklerle verilen test ve online test bölümlerini ziyaret etmenizi tavsiye ediyoruz…

Gerçek Sayılar:

a,b birer tamsayı ve b sıfırdan farklı olmak üzere $\large \frac{a}{b}$ şeklinde yazılamayan sayılara irrasyonel sayılar denilir.İrrasyonel sayılar kümesi “ $\large \mathbb{I}$ ” ile gösterilir.

$\pi$ ve $\large \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{8},\sqrt{10}.....$ gibi kök dışına çıkamayan sayılar irrasyonel sayılardır.

Örnekler:

$\sqrt{1}$ : bir irrasyonel sayı değildir. Zira kök dışına 1 olarak çıkar

$\large \sqrt{4}$ : bir irrasyonel sayı değildir. Zira kök dışına 2 olarak çıkar

$\large \sqrt{3}$ : bir irrasyonel sayı dır. Zira kök dışına tam sayı olarak çıkamaz.

$\large \sqrt{5}$ : bir irrasyonel sayı dır. Zira kök dışına tam sayı olarak çıkamaz.

Sayıları küme olarak gösterirsek;

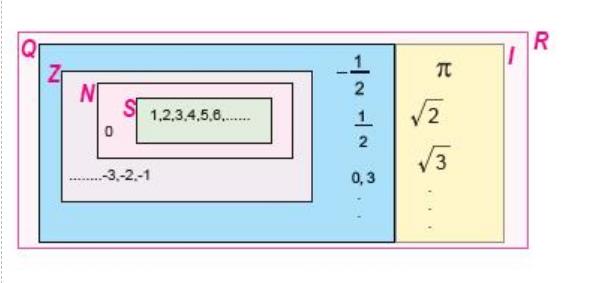Rasyonel sayılar ile irrasyonel sayılar kümesi bir araya gelirse reel(gerçek ) sayılar kümesini oluştururlar.

$\large Q\cup \mathbb{I}=\Re$

$\large S\subset N \subset Z \subset Q \subset R$

En büyük küme R : Reel(Gerçek) sayılar kümesidir.

SONUÇLAR:

Her sayı aynı zamanda bir reel sayıdır
$\pi$ bir irrasyonel sayı aynı zamanda bir reel sayıdır
$\large \sqrt{3}$ bir irrasyonel sayı aynı zamanda bir reel sayıdır
Her rasyonel sayının bir ondalık gösterimi vardır.
Her ondalık gösterim ,rasyonel sayı olarak yazılabilir.
$\large \sqrt{0}=0$ olduğundan , $\large \sqrt{0}$ bir rasyonel sayıdır.
Eğer bir işlem verilirse önce işlemin sonucu bulunur sonra hangi kümeye ait olduğu tespit edilir.

Örnek: $\large \sqrt{9}+\frac{1}{2}$ ifadesi bir irrasyonel sayımıdır?

Çözüm: $\large \sqrt{9}=3$ olduğundan , sonuç= $\large 3+\frac{1}{2}=\frac{7}{2}$ olarak bulunur ki bu da rasyonel olduğunu gösterir.

Örnek: $\large 3+\sqrt{5}$ ifadesi bir irasyonel sayı mıdır?

Çözüm: $\large \sqrt{5}$ kök dışına tam sayı olarak çıkamaz. $\large \sqrt{5}$ bir irrasyonel sayıdır.İrrasyonel sayı ile herhangi bir sayının toplamı veya farkı yine irrasyonel sayı olur.

Örnek: $\sqrt{2}.\sqrt{8}$ ifadesi bir irrasyonel sayı mıdır?

Çözüm: $\large \sqrt{8}.\sqrt{2}=\sqrt{16}=4$

olduğundan $\large \sqrt{8}.\sqrt{2}$ irrasyonel sayı değildir. $\large \sqrt{8}.\sqrt{2}$ (4 olarak kabul ederiz) sayısı hem doğal sayı,hem sayma sayısı hem tam sayı hemde rasyonel sayıdır.

İrrasyonel Sayıyı Rasyonele Çevirme: