8.Sınıf Öteleme, Yansıma ve Dönme Konu Anlatımı

8.Sınıf Matematik Öteleme, Yansıma ve Dönme Konu Anlatımı, önemli hatırlatmalar ve sık karşılaşılan örneklerle konuyu özetler niteliktedir.

Öteleme, Yansıma ve Dönme

Öteleme

Koordinat düzleminde bir nokta x ekseninde sağa ve sola, y ekseninde aşağı ve yukarı ötelenebilir.

A(x,y) noktası ;

Sağa öteleniyorsa x artar
Sola öteleniyorsa x azalır
Yukarı öteleniyorsa y artar
Aşağı öteleniyorsa y azalır

Yani;

Koordinat düzleminde;A(a, b) noktasının;
• x ekseninde 3 br sağa ötelenmesiyle A'(a + 3, b) noktası elde edilir.
• x ekseninde 2 br sola ötelenmesiyle A'(a – 2, b) noktası elde edilir.
• y ekseninde 4 br yukarı ötelenmesiyle A'(a, b + 4) noktası elde edilir.
• x ekseninde 2 br sağa ve y ekseninde 3 br aşağı ötelenmesiyle A'(a + 2 , b – 3) noktası elde edilir.

Örnek:

Köşe koordinatları A(1, –4), B(5, –3) ve C(3, –5) olan ABC üçgeninin x ekseninde 4 br sola, y ekseninde 5 br yukarı ötelenmesiyle oluşan A’B’C’ üçgeninin köşe koordinatlarını bulunuz.

Çözüm:

Noktaların x bileşenleri 4 br azaltılır ve y bileşenleri 5 br arttırılır.
A(1, –4) → A'(1 – 4, –4 + 5) = A'(–3, 1)
B(5, –3) → B'(5 – 4, –3 + 5) = B'(1, 2)
C(3, –5) → C'(3 – 4, –5 + 5) = C'(–1, 0)
Buradan A'(–3, 1), B'(1, 2) ve C'(–1, 0) olur.

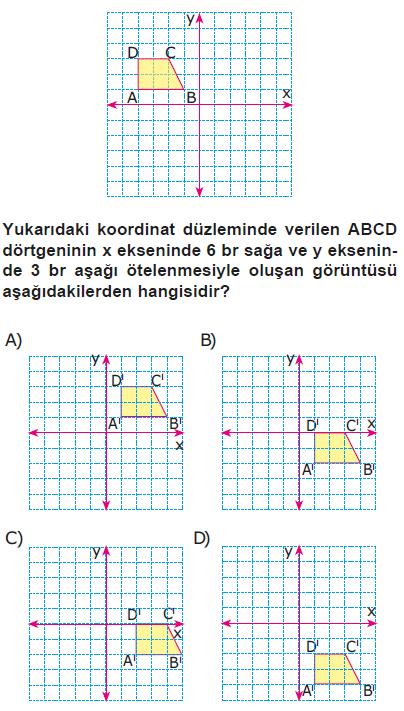
Örnek:

Öteleme

Çözüm:

ABCD dörtgeninin köşe koordinatları yazılıp 6 br sağa
ve 3 br aşağı öteleme yapılırsa;
A(–4, 1) → A'(–4 + 6, 1 –3) = A'(2, –2)
B(–1, 1) → B'(–1 + 6, 1 – 3) = B'(5, –2)
C(–2, 3) → C'(–2 + 6, 3 – 3) = C'(4, 0)
D(–4, 3) → D'(–4 + 6, 3 – 3) = D'(2, 0)
A’B’C’D’ dörtgeninin görüntüsü C şıkkında doğru verilmiştir.

Yansıma

Koordinat düzleminde A(5, 3) noktasının x eksenine göre yansıması B, y eksenine göre yansıması C ve orjine göre yansıması olan D noktalarını çizelim.

A(x.y) noktasının ;

xx’ eksenine göre yansımasında noktanın y değeri işaret değiştirir.
yy’ eksenine göre yansımasında noktanın x değeri işaret değiştirir.
orjine göre yansımasına x ve y değeri işaret değiştirir.

Örnek:

A( 3,4) noktasının xx’ eksenine göre yansıması sonucu oluşan nokta A'(3,-4) tür.

A( 3,4) noktasının yy’ eksenine göre yansıması sonucu oluşan nokta A'(-3,4) tür.

A( 3,4) noktasının orjine eksenine göre yansıması sonucu oluşan nokta A'(-3,-4) tür.

Dönme

**Önce koordinatların yerlerini değiştir.

**Sonra dönüş yönündeki koordinatın işaretini değiştir.

Örnek:A(-4,2) noktasını 90 derece sağa döndürelim;

**Önce yerdeğiş>> (2,-4)

**Sonra,sağa döndüğümüz için sağdakinin işaretini değiştir>> (2,4)

Örnek: A(-4,2) noktasını 90 derece sola döndürelim;

**Önce yerdeğiş>> (2,-4)

**Sonra,sola döndüğümüz için soldakinin işaretini değiştir>> (-2,-4)

180 Derece dönme:

**Koordinatların sadece işaretleri değişir

Örnek: A(-4,2) noktasını 180 derece döndürelim;

A(-4,2) noktasının işaretlerini değiştirirsek; A’(4,-2) olarak bulunur.

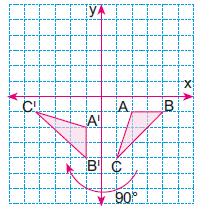
Örnek:

Köşe koordinatları A(2, –1), B(4, –1) ve C(1, –4) olan ABC üçgeninin orijin etrafında saat yönünde 90° döndürülmesiyle oluşan A’B’C’ üçgeninin koordinatlarını bulunuz. Görüntüsünü çiziniz

Çözüm:

90 derece sağa dönme örnek