matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi
6.Sınıf Kesişim ve Birleşim Kümesi Kavramları Konu Anlatımı
- Kesişim Kümesi
- Birleşim Kümesi
Kavramlarından oluşmaktadır.
| İlgili Kazanım: M.6.1.3.1. Kümeler ile ilgili temel kavramları anlar. |
Kesişim Kümesi
| İki veya daha fazla kümenin ortak elemanlarının oluşturduğu kümeye kesişim kümesi denir Kesişim,” ∩ “sembolü ile gösterilir |
| örnek: A = { 1, 3, 5, 6, 7, 8, 9} ve B = { 2, 3, 4, 6, 8,9,10} kümeleri veriliyor. Buna göre A ∩ B kümesini bulalım. Çözüm: A = { 1, 3, 5, 6, 7, 8, 9} ve B = { 2, 3, 4, 6, 8 , 9 , 10} Yukarıdaki A ve B kümelerinin (ikisininde elamanı olan) ortak elamanları : 3 , 6 , 8 , 9 A ∩ B = { 3 , 6 , 8 , 9 } |
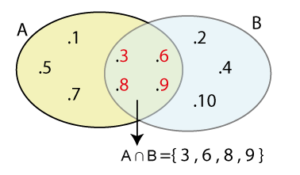
| Örnek: A = { 1, 3, 5, 6, 7, 8, 9} ve B = { 2, 3, 4, 6, 8,9,10} kümeleri veriliyor. Buna göre A ∩ B kümesini venn şemasında gösterelim Çözüm: A = { 1, 3, 5, 6, 7, 8, 9} ve B = { 2, 3, 4, 6, 8 , 9 , 10} Yukarıdaki A ve B kümelerinin (ikisininde elamanı olan) ortak elamanları : 3 , 6 , 8 , 9
|
| Kesişim kümesinin elaman sayısı s(A∩B) sembolüyle gösterilir. |
| Örnek: A = { 3 , 5 , 7 , 9 , 11 , 13 , 15 } ve B = { 3 , 6 , 9 , 12 , 15 } kümeleri veriliyor. Buna göre s(A∩B)=? Çözüm: A = { 3 , 5 , 7 , 9 , 11 , 13 , 15 } ve B = { 3 , 6 , 9 , 12 , 15 } A ∩ B = { 3 , 9 , 15 } ve s(A∩B)= 3 |
Birleşim Kümesi
| İki veya daha fazla kümenin tüm elemanlarının birleştirilmesiyle oluşturulan kümeye birleşim kümesi denir. Birleşim ” ∪ ” sembolü ile gösterilir. |
| Örnek: A= { 1 , 5 , 6 , 7 , 8 , 9} ve B={7 , 8 , 9 , 10 , 11 , 12 } kümeleri veriliyor. Buna göre AUB (A birleşim B) kümesini bulunuz. Çözüm: İki kümenin elemanlarını birleştirelim (Aynı elamanlardan sadece birini alabiliriz.Çünkü bir kümede aynı elaman iki defa yazılamaz!) AUB = {1 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 } şeklindedir. |
| Birleşim kümesinin elaman sayısı s(AUB) sembolüyle gösterilir. |
| Yukarıdaki AUB = {1 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 } kümesinin elaman sayısı s(AUB)=9 ‘dur. |
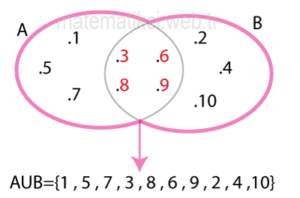
| Örnek: A = { 1, 3, 5, 6, 7, 8, 9} ve B = { 2, 3, 4, 6, 8,9,10} kümeleri veriliyor. Buna göre A U B kümesini venn şemasında gösterelim Çözüm:
|
6.Sınıf Matematik Konu Anlatımı için>>
6.Sınıf Matematik Testi indirmek için>>
