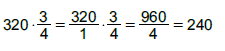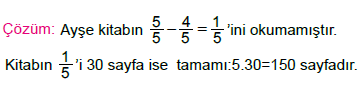7.Sınıf Rasyonel Sayılarla Problemler Konu Anlatımı

7.sınıf Matematik Rasyonel Sayılarla Problemler Konu Anlatımı güncel müfredata uyumludur,örnek ve çözümler güncel kitaplardaki sorularla benzerdir.Öğrenci seviyesine uygun olarak konu anlatılmıştır.

Rasyonel Sayılarla Problemler:

Örnek: 320’nin $\small \frac{3}{4}$ ‘ü kaçtır?

Çözüm:

1.yol:Bir varlığın kesir kadarı , varlıkla kesrin çarpımı kadardır.

2.Yol: Paydaya böl, pay ile çarp.

320 : 4 =80

80 x 3=240

Rasyonel Sayılarla Problemler

Örnek:

Bir memur maaşının $\small \frac{1}{6}$ ’ini ev kirasına , $\small \frac{3}{10}$ ’ünü

faturalara , $\small \frac{7}{15}$ ’ini de kredi ödemesi olarak bankaya yatırıyor.

Geriye 120 TL parası kaldığına göre memurun maaşı kaç TL dir?

Çözümü Göster

Örnek:

Ayşe bir kitabın $\small \frac{4}{5}$ ’ini okuyor.

Geriye 30 sayfa kaldığına göre kitabın tamamı kaç sayfadır?

Çözümü Göster

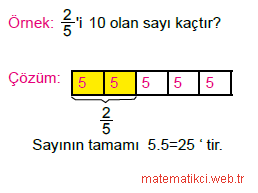
Örnek:

Hüseyin parasının $\small \frac{1}{3}$ ’üne defter, $\small \frac{1}{4}$ ’ine kalem
almıştır.Geriye 10 TL parası kaldığına göre ,parasının
tamamı kaç TL’dir.

Çözümü Göster

Örnek:

7 de 4 ’ü dolu olan bir depodan 10 litre su çekilirse ,deponun yarısı boş kalıyor.

Depodaki su miktarı başlangıçta kaç litredir?

Çözümü Göster

Çözüm:

Depoyu 7 eşit bölme kabul edersek yarısı 3,5 bölme olur.
Virgülle uğraşmamak için kesri genişletelim.
Depoyu 14 eşit bölmeye ayırırsak 8 bölmesi su ile doludur.
Deponun yarısı 7 bölmeden oluşur.8 bölmede su varken 10 litre su çekilince 7 bölmeye düşmüş.
Ohalde 1 bölme 10 litre demektir.
Başlangıçta depoda 8 bölme su varmış , bu da 8.10 = 80 litreye karşılık gelir.

Örnek:

60 teneke sıvı yağ , teneke hacminin $\small \frac{3}{5}$ ’i büyüklüğündeki cam şişelere doldurularak satışa sunulacaktır.

Bu iş için kaç cam şişe gereklidir?

Çözümü Göster

NOT: Çubuk, tel , ip kesilmesi sorularında , orta nokta kesilen parçanın uzunluğunun yarısı kadar kayar.

Örnek:

120 cm uzunluğundaki bir ipin uç noktasından 30cm lik kısmı kesiliyor.

İpin orta noktası kaç cm kayar?

Çözümü Göster

Çözüm:

Kesilen parça 30 cm olduğuna göre , orta nokta 30 : 2 = 15 cm kayar.

Örnek:

Bir telin ucundan , $\small \frac{1}{6}$ ‘i kesiliyor , orta noktası 15cm kaydığına göre , telin kesilmeden önce uzunluğu kaç cm dir?

Çözümü Göster

Çözüm:

Telin orta noktası kesilen parçanın yarısı kadar kayar.
Bu bilgiye göre 15 cm kayma olmuşsa , kesilen parçanın boyu 30 cm demektir.
Buradan telin $\small \frac{1}{6}$ ’nin 30 cm olduğu ortaya çıkar.
Telin tamamı 30 . 6 = 180 cm dir.

Rasyonel sayılarla problemler ilgili daha çok test çözmek için>>

Rasyonel Sayılarla problemler ile ilgili Test indirmek için>>

Rasyonel Sayılarla problemler ile ilgili daha çok dökümana ulaşmak için>>

matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi

7.Sınıf Rasyonel Sayılarla Problemler Konu Anlatımı

Rasyonel Sayılarla Problemler:

İlgili Makaleler

Bunlar da İlgini çekebilir

7.Sınıf Rasyonel Sayılar Konu Anlatımı

7.Sınıf Matematik Rasyonel Sayılar Testi Çöz

Abone Ol

7.Sınıf Rasyonel Sayılarla Problemler Konu Anlatımı

Rasyonel Sayılarla Problemler:

İlgili Makaleler

7.Sınıf Rasyonel Sayılarla Çok Adımlı İşlemler Testi İndir

7.Sınıf Matematik Rasyonel Sayılar Testi indir

7.Sınıf Rasyonel Sayılar Kazanım Kontrol Testi İndir

Bunlar da İlgini çekebilir

7.Sınıf Rasyonel Sayılar Konu Anlatımı

7.Sınıf Matematik Rasyonel Sayılar Testi Çöz

Abone Ol