matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi
8.Sınıf Matematik Birinci Dereceden Bir Bilinmeyenli Denklemler konu anlatımında, uyarı ve notlarla konuyu açıklayan örneklerle kolay bir anlatım amaçlanmıştır.
| Birinci Dereceden Bir Bilinmeyenli Denklemler |
Bir denklemde bilinmeyeni bulmak için yapılan işlemlere denklemi çözme denir.
|
| Örnek: 3x – 4 = 17 denklemini çözelim 3x-4 +4 = 17 + 4 (Eşitliğin her iki tarafına aynı +4 ekleyebiliriz) 3x=21 (eşitliğin her iki tarfını 3 ile bölebiliriz) x=7 |
Kısa yolu: 3x – 4=17 ise -4 tü eşitliğin karşısına atarız.
(Eşitliğin karşısına giden sayı işaret değiştirir)
3x= 17 +4
3x=21 (x’i yalnız bırakmak için,eşitliğin her iki tarafını 3 ile bölelim)
x=7 bulunur.
Örnek: 3.(x – 3) – 4 = 17 denklemini çözelim
Çözüm:
3x – 3.3 – 4=17
3x – 9 – 4=17
3x – 13=17
3x =17+13
3x=30
x=10
Örnek: 5 · (x – 2) = 3 · (2x + 1) denkleminde x=?
-10 -3 = 6x – 5x
-13=x bulunur.
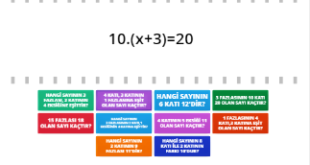
Örnek: denkleminin çözümünü bulunuz
Çözüm:
8.Sınıf Matematik Konu Anlatımına ait diğer başlıklar için>>
8.Sınıf Matematik ile ilgili çok test çözmek için>>
8.Sınıf Matematik ile ilgili Test indirmek için>>
8.Sınıf Matematik ile ilgili daha çok dökümana ulaşmak için>>
