8.sınıf matematik Doğrusal Denklemlerin Grafiğini Çizme Konusu, önemli bilgileri içeren notlar ve hatırlatmalarla desteklenmiş,örneklerle anlaşılır bir anlatım yapılmıştır.
| Doğrusal Denklemler |
| x ve y değişken, a ve b katsayı ve c sabit terim olmak üzere: ax + by + c = 0 biçiminde olan denklemlere doğrusal denklem denir. |
| Doğrusal denklemde a ve b katsayılarının ikisi birden 0 olamaz.Yani denklemde en az bir tane bilinmeyen bulunmalıdır. a ve b sıfırdan farklı olmak sayılar olmak üzere ax+by+c=0 gibi,x ve y değişkeninin kullanıldığı eşitliklere doğrusal denklem denilir. |
| Örnek: 2x+3y=24 ifadesi bir doğrusal denklemdir. Örnek: x=7 bir doğrusal denklemdir. Örnek: y=-4 bir doğrusal denklemdir. Örnek: y=5x bir doğrusal denklemdir. |
| Doğrusal ilişkiyi gösteren denklemlerin grafiği doğru grafikleridir |
| Doğrusal Denklemlerin Grafiğini Çizme |
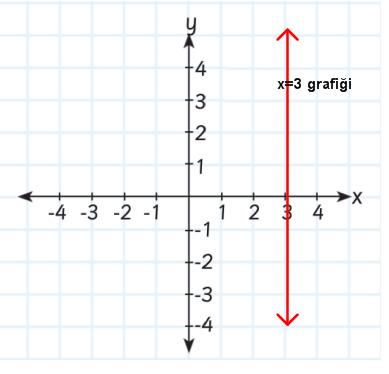
| a)Eksenlere paralel olan doğruların grafikleri: Örnek: x=3 doğrusunun grafiğini çizelim
|
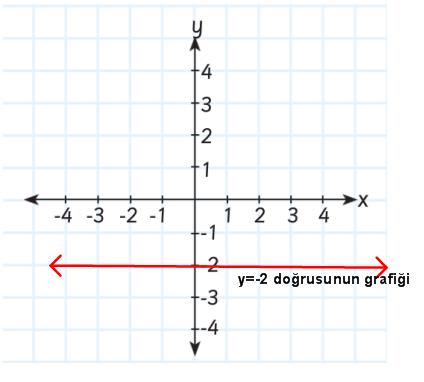
| Örnek: y=-2 doğrusunun grafiğini çizelim
|
b)Orjinden geçen doğruların grafiklerini çizmey=ax tarzındaki denklemlerin grafikleri orjinden geçer. Diğer bir deyişle; Örnek: |
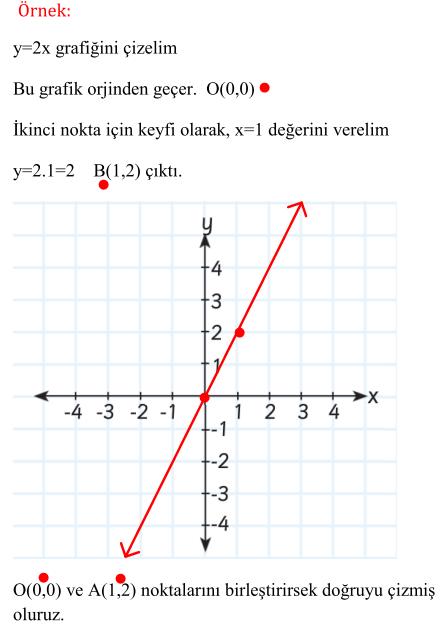 |
 |
 |
| Not:Bir noktanın x ve y değerleri denklemin eşitliğini sağlıyorsa; o nokta doğru üzerindedir denilir. |
| Örnek: A(1,2) noktası x+2y-5=0 doğrusu üzerinde midir?Çözüm:A(1,2) noktasında x=1 ve y=2 dir.Bu değerleri denklemde yerine koyalımx+2y-5=0 eşitliğini sağlayıp sağlamadığını kontrol edelim 1+2.2-5=0 eşitliğini sağlıyor o halde A noktası x+2y-5=0 doğrusunun üzerindedir denilir.(veya A noktası x+2y-5=0 doğrusuna ait bir noktadır denilir) |
| Örnek: A(4,1) noktası x-2y-m=0 doğrusu üzerinde ise m=?Çözüm:A noktası x-2y-m=0 doğrusu üzerinde ise ; denklemde x=4 ve y=1 yerine konulduğunda eşitliği sağlıyor demektir.x-2y-m=0 4-2.1-m= 2-m=0 m=2 olarak bulunur. |
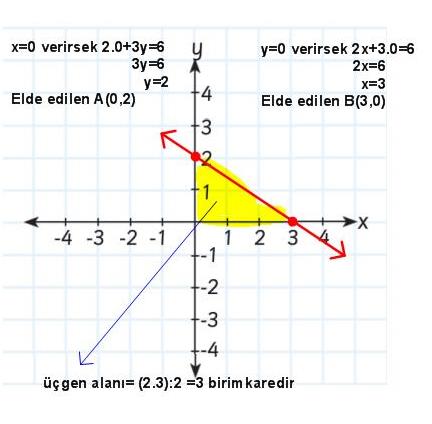
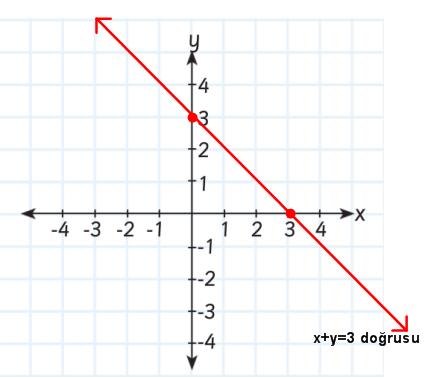
Örnek:
2x+3y=6 grafiği ve eksenler arasındaki kalan bölgenin alanı kaç br2 dir?
| Çözüm:
|
8.Sınıf Matematik Konu Anlatımına ait diğer başlıklar için>>
8.Sınıf Matematik ile ilgili çok test çözmek için>>
8.Sınıf Matematik ile ilgili Test indirmek için>>
8.Sınıf Matematik ile ilgili daha çok dökümana ulaşmak için>>
 matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi
matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi