8.Sınıf Matematik Eşitsizliklerin Çözümü Konu Anlatımı, önemli hatırlatmalar ve sık karşılaşılan örneklerle konuyu özetler niteliktedir.
| Eşitsizliklerin çözümü Konu Anlatımı |
| Bir eşitsizliğin her iki tarafına aynı sayı eklenir veya her iki tarafından aynı sayı çıkarılırsa eşitsizlik bozulmaz. Bu kural hatırlanacağı üzere denklemler için de geçerliydi. |
 |
| Not:(kısayol) Eşitsizlikler çözerken, denklemlerin çözümüne benzer biçimde yapabiliriz. Mesela eşitsizliğin her iki tarafına sayı eklemek yerine , eşitsizlikte karşıya atılan sayının işaret değiştirmesi yöntemini kullanabiliriz. Bu taktik soru çözerken bize zaman kazandırır. Örnek: x+6 < 10 işleminde x’i yalnız bırakmak için önce +6 yı karşıya işaret değiştirerek göndeririz x < 10-6 buradan kısaca x < 4 bulunur. |
| Kural: Bir eşitsizliğin her iki tarafı pozitif bir sayı ile çarpılır veya bölünürse eşitsizlik bozulmaz Bu kural hatırlanacağı üzere denklemler için de geçerliydi. |
| Örnek:
Çözüm: Ç={ x \ |
| NOT Bir eşitsizliğin her iki tarafı negatif bir sayı ile çarpılır veya bölünürse eşitsizlik yön değiştirir. Sebebi: -3 < -2 ifadesinin her iki tarafını (-1) ile çarparsak ve yön değiştirmezsek ifade; +3 <+2 gibi yanlış bir sonuç ortaya çıkar.Böyle yanlışlıklara sebebiyet vermemek için yön değiştirilir. Bu özellik bu konunun en önemli özelliğidir.Çözümde denklem gibi davranıp bu özelliği gözden kaçırırsanız soru çözümü yanlış olacaktır. Eşitsizlik negatif bir sayı ile çarpıldığı an eşitsizlik yönü değiştirilmelidir. Eşitsizlik negatif bir sayı ile bölündüğü an eşitsizlik yönü değiştirilmelidir. |
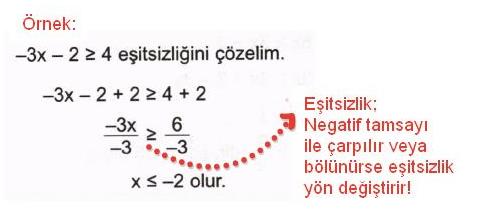 |
 |
| Not: Eşitsizlikte,sorunun çözümü hangi kümede isteniyorsa o kümeye ait değerler dikkate alınır. Eğer çözüm için herhangi bir kümeden bahsetmemiş ise bu durumda Reel sayılarda çözüm yapılacak demektir. |
 |
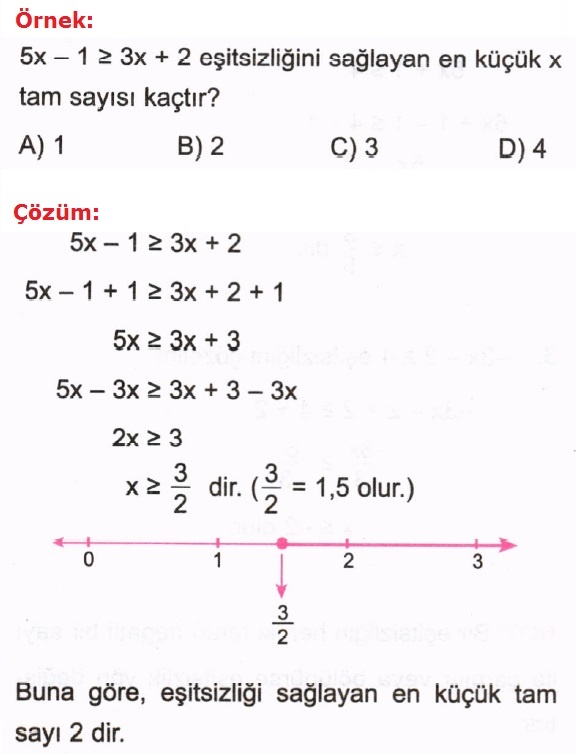 |
8.Sınıf Matematik ile ilgili çok test çözmek için>>
8.Sınıf Matematik Konu Anlatımına ait diğer başlıklar için>>
8.Sınıf Matematik ile ilgili Test indirmek için>>
8.Sınıf Matematik ile ilgili daha çok dökümana ulaşmak için>>
 matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi
matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi

