8.Sınıf Kareköklü Sayıların Sayı Doğrusundaki Yeri

8.Sınıf Matematik Kareköklü Sayıların Sayı Doğrusundaki Yeri Konu Anlatımı güncel müfredata uygun olarak , kitaplardaki popüler soruların benzerleri dikkate alınarak hazırlanmıştır.Konu sonunda linklerle verilen test ve online test bölümlerini ziyaret etmenizi tavsiye ediyoruz…

Kareköklü Sayıların Sayı Doğrusundaki Yeri:

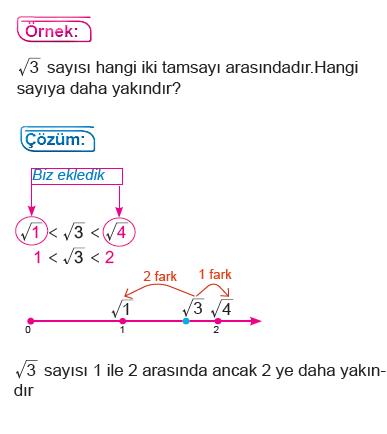
Kareköklü sayıya yakın olan,kök içleri tamkare sayı olacak şekilde kareköklü sayılar yerleştirilir.
Tamkare sayılar kökten çıkarılır ve kareköklü ifadenin hangi sayılar arasında olduğu bulunur.

Örnek:

$\large \sqrt{13}$ sayısının değeri hangi iki tam sayı arasındadır?

Çözüm:

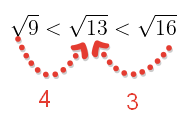
$\large \sqrt{13}$ yakınında bulunan kök dışına tam sayı çıkabilecek şekilde kare köklü sayılarla alttan ve üstten sınırlayalım.

$\large \sqrt{9}<\sqrt{13}<\sqrt{16}$

$\large 3<\sqrt{13}<4$

Görüldüğü gibi $\large \sqrt{13}$ sayısı $\large \sqrt{16}=4$ sayısına daha yakındır.Yani $\large \sqrt{13}$ sayısı 3,5 ile 4 arasındadır.

Örnek:

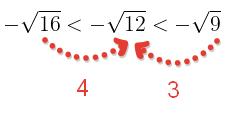
$\large -2\sqrt{3}$ sayısının değeri hangi iki tam sayı arasındadır?

Çözüm:

$\large -2\sqrt{3}=-\sqrt{2^{2}.3}=-\sqrt{12}$

$\large -\sqrt{16}<-\sqrt{12}<-\sqrt{9}$

$\large -4<-\sqrt{12}<-3$

$\large -\sqrt{12}$ sayısı -3 ile -4 arasındadır.Ancak -3 ‘e daha yakındır. -3,5 ile -3 arasındadır diyebiliriz.

Kareköklü Sayıların Tahmini Değeri

Örnek:

$\large \sqrt{3}$ sayısının yaklaşık değerini bulalım

Çözüm:

$\large \sqrt{1}<\sqrt{3}<\sqrt{4}$

$\large \sqrt{3}\sim \sqrt{1}+\frac{3-1}{4-1}$

$\large \sqrt{3}\sim \1+\frac{2}{3}$

$\large \sqrt{3}\sim \frac{5}{3}=1,6..\sim1,7$

Kareköklü sayıların yaklaşık değeri soruları daha çok yakınlık olarak sorulmaktadır.hangi sayıya yakındır şeklinde sorular gelmektedir.Yukarıdaki yaklaşık tahmin sorularda fikir vermesi amacıyla alternatif bir yol olarak verilmiştir.

Örnek:

$\large \sqrt{2}\cong 1,4$ olduğuna göre $\large \sqrt{18}$ in yaklaşık değerini bulunuz.