matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi
8.Sınıf Matematik Üçgen Eşitsizliği Konu Anlatımı , önemli hatırlatmalar ve sık karşılaşılan örneklerle konuyu özetler niteliktedir.
| Üçgen Eşitsizliği |
| Bir üçgenin kenarlarından birinin uzunluğu; diğer iki kenarının uzunlukları toplamından küçük,uzunlukları farkının mutlak değerinden büyüktür. |
 |
Yukarıdaki tanımın pratik yolu:Her zaman büyük kenardan küçük kenarı çıkarırsak mutlak değer almamıza gerek kalmayacaktır.Aşağıdaki örneklerde büyük kenardan küçük kenar çıkarılmış,mutlak değeri almaya gerek kalmamıştır.
| Örnek:
|
| Yukarıdaki ABC üçgeninin AC kenarı hangi tam sayı değerlerini alabilir? |
Çözüm:
x = 4 , 5 , 6 , 7 , 8 , 9 , 10 değerlerini alabilir.
| Örnek:
|
Çözüm:
BC kenarının uzunluğuna x dersek.
Eğer ABC üçgeni eşkenar üçgen olsaydı iç açıları 600 ve kenar uzunlukları 8 cm olurdu.
Yani A açısı 600 lik açı olsaydı BC kenarı 8 cm olurdu.
A açısı 600 den küçük verilmiş o halde BC kenarı da 8 cm den küçük olmalıdır.(Büyük açı karşısında büyük kenar olur)
Bu durumda BC kenarı
şeklinde olmak zoruna kalır.En büyük x tamsayı değeri 7 olarak bulunur.
| Örnek:
|
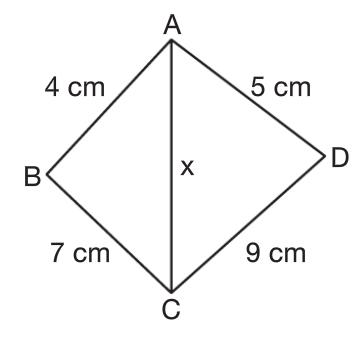
| Yukarıdaki ABCD dörtgeninde AC kenarının alabileceği tam sayı değerlerini bulunuz. |
Çözüm:
Soldaki üçgen için,üçgen eşitsizliği kuralım:
Sağdaki üçgen için,üçgen eşitsizliği kuralım:
İki eşitsizliğin sonucu olarak
x değerleri 5 , 6 , 7 , 8 , 9 , 10 olabilir. |
| Örnek:
|
| Yukarıdaki üçgenlere göre BC kenarının alabileceği tam sayı değerlerini bulunuz. |
Çözüm:
BDC üçgeni için üçgen eşitsizliğini kuralım:
BC kenarının uzunluğuna x dersek;
ABC üçgeni için üçgen eşitsizliğini kuralım:
| İki eşitsizliğin sonucu olarak;
|
8.Sınıf Matematik Konu Anlatımına ait diğer başlıklar için>>
8.Sınıf Matematik ile ilgili çok test çözmek için>>
8.Sınıf Matematik ile ilgili Test indirmek için>>
8.Sınıf Matematik ile ilgili daha çok dökümana ulaşmak için>>
