Perşembe , Aralık 5 2024

matematikci.web.tr Matematik,Konu Anlatımı,Test ve Deneme Arşivi

DUYURU:

Ana Sayfa / Matematik / Ortaokul / 8.Sınıf Matematik / 8.Sınıf-Üslü Sayılar / 8.Sınıf Üslü İfadelerde Bölme İşlemi Konu Anlatımı

8.Sınıf Üslü İfadelerde Bölme İşlemi Konu Anlatımı

8.Sınıf-Üslü Sayılar 1,720 Views

8.Sınıf Matematik Üslü İfadelerde Bölme İşlemi Konu Anlatımı güncel müfredata uygun olarak , kitaplardaki popüler soruların benzerleri dikkate alınarak hazırlanmıştır.Konu sonunda linklerle verilen test ve online test bölümlerini ziyaret etmenizi tavsiye ediyoruz…

Anlatımın içeriği;

Tabanları aynı olan üslü sayılarda bölme işlemi tanımı ve örnekleri
Tabanları farklı üslü ifadenin bölme işlemi örnekleri
Tabanları farklı üsleri aynı olan üslü ifadelerin bölümü(ortak üs kuralı) tanımı ve örnekleri

Üslü Sayılar konusu 8.sınıf matematik konuları içerisinde en önemli konudur. Kareköklü sayılar,çarpanlar katlar,cebirsel ifadeler konularında üslü sayıların bilgilerine ihtiyaç vardır.Bu sebeple bu konunun iyi anlaşılması gerekir.

Bu konuda mümkün olduğunca fazla soru çözüp,konuyu pekiştirmenizi tavsiye ediyorum.

Üslü İfadelerde Bölme İşlemi

Tabanları aynı olan üslü ifadelerde bölme işleminde;

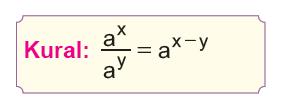Payın kuvvetinden ,paydanın kuvveti çıkarılır ve sonucun kuvveti olarak yazılır.

Örnekler:

$\frac{2^{10}}{2^{6}}=2^{10-6}=2^{4}$

$\frac{3^{-4}}{3^{6}}=3^{-4-6}=3^{-10}$

$\frac{5^{7}}{5^{-6}}=5^{7-(-6)}=5^{7+(+6)}=5^{13}$

SoruCevap

$\frac{3^{12}}{3^{5}}=?$

$3^{12-5}=3^{7}$

Eğer tabanlardan biri parantezli, diğeri parantezsiz verilmiş ise;

Parantezli taban parantezsiz taban haline dönüştürülerek,(tabanlar aynı hale getirilerek) işleme başlanır.

Örnek:

$\frac{2^{10}}{(-2)^{8}}=\frac{2^{10}}{2^{8}}=2^{10-8}=2^{2}=4$

SoruCevap

$\frac{2^{9}}{(-2)^{3}}=?$

$\frac{2^{9}}{{\color{Red} (-2)^{3}}}=\frac{2^{9}}{\color{Red} {-2^{3}}}=-2^{9-3}=-2^{6}$

Örnek:

$\frac{-3^{6}}{(-3)^{7}}=?$ işleminin sonucunu bulunuz.

Çözüm:

$\frac{-3^{6}}{(-3)^{7}}=\frac{-3^{6}}{-3^{7}}=\frac{3^{6}}{3^{7}}=3^{6-7}=3^{-1}=\frac{1}{3}$

Üslü Sayılarda Bölme İşlemi-Ortak Üs:

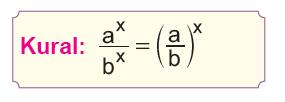Üsler aynı ise ; tabanlar bölünür, sonucun tabanı olarak yazılır , üs aynı kalır

Örnekler:

$\frac{6^{10}}{3^{10}}=\left ( \frac{6}{3} \right )^{10}=2^{10}$

$\frac{9^{6}}{3^{6}}=\left ( \frac{9}{3} \right )^{6}=3^{6}$

$\frac{12^{9}}{4^{9}}=\left ( \frac{12}{4} \right )^{9}=3^{9}$

SoruCevap

$\frac{6^{9}}{3^{9}}=?$

$\frac{6^{{\color{Red} 9}}}{3^{{\color{Red} 9}}}=\left ( \frac{6}{3} \right )^{{\color{Red} 9}}=2^{{\color{Red} 9}}$

Eğer tabanlardan birisi parantezli gelmişse;

Önce parantezli tabanlar parantezsiz tabana çevrilir,sonucun işareti belirlenir
Sonra kural yukarıdaki uygulanır.

Örnek:

$\frac{-30^{6}}{(-15)^{6}}=\frac{-30^{6}}{15^{6}}=-\left ( \frac{30^{6}}{15^{6}} \right )=-\left ( 2^{6} \right )=-2^{6}$

Örnek:

$\frac{(-15)^{13}}{(-3)^{13}}= \frac{-15^{13}}{-3^{13}}=+\left ( \frac{15}{3} \right )^{13}=+5^{13}$

8.Sınıf Matematik Üslü Sayılar Konu Anlatımı ilgili daha çok test çözmek için>>

8.Sınıf Matematik Üslü Sayılar Konu Anlatımı ile ilgili Test indirmek için>>

8.Sınıf Matematik Üslü Sayılar Konu Anlatımı ile ilgili daha çok dökümana ulaşmak için>>

İlgili Makaleler

Bunlar da İlgini çekebilir

8.Sınıf Üslü İfadeler Konu Anlatımı

8.Sınıf Üslü İfadeler Konu Anlatımı 8.Sınıf Üslü İfadeler konusu sekizinci sınıfın ikinci konudur. Bu konuya …

Üslü Sayı işlem Oyunu