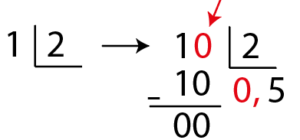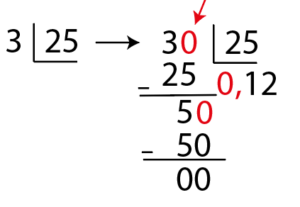6.Sınıf Ondalık Gösterimin Bölme İle İlişkisi Konu Anlatımı ile ilgili kazanımlar- M.6.1.6.1. Bölme işlemi ile kesir kavramını ilişkilendirir.
|
| Ondalık Kesirlerin Bölme ile ilişkisi |
- 4 : 2 okunuşu : “4 bölü 2”
- \(\large \frac{4}{2}\) : “Okunuşu 4 bölü 2”
- okunuşları aynı olan bu iki ifade birbirine eşittir.
- Yani: \(\large \frac{4}{2}\) = 4 : 2 yazılabilir.
|
Bir kesri ondalık hale getirmek için 2 farklı yolumuz var.- 1.Yol: Kesrin payını ve paydasını genişleterek veya sadeleştirerek 10,100. 1000 haline getiririz.
- Örnek: \(\large\frac{1}{2}=\frac{5}{10}=0,2\)
|
- 2.Yol: Kesrin payını, paydasına bölerek ondalık hale getiririz.
- Örnek: \(\large\frac{1}{2}= 1 : 2=0,2\)

|
| Örnek:
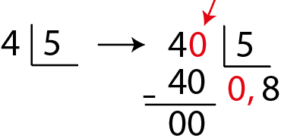
\(\large \frac{4}{5}\) ifadesinin ondalık gösterimini bulalım. Çözüm: 1.Yol: - Kesrin paydası 10 yapılabilir.
\(\large \frac{4}{5}=\frac{8}{10}=0,8\) | Çözüm: 2.Yol: 
|
| Örnek:
\(\large \frac{3}{25}\) ifadesinin ondalık gösterimini bulalım. Çözüm: 1.Yol: - Kesrin paydası 100 yapılabilir.
\(\large \frac{3}{25}=\frac{12}{100}=0,12\) | Çözüm: 2.Yol: 
|
[ads2]
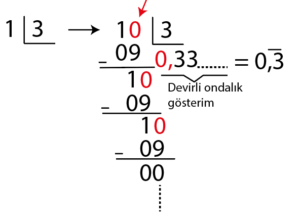
Devirli Ondalık Gösterim
- Bazen kesrin paydası genişletme veya sadeleştirme yoluyla 10,100,1000 yapılamaz.
- Böyle durumlarda payını bölme işlemiyle paydasına böleriz.
- Eğer bölüm sürekli aynı sayı olacak şekilde virgülün sağında devam ediyorsa böyle ifadelere devirli ondalık gösterim denilir.
|
| Örnek: \(\large\frac{1}{3}\) kesrinin ondalık gösterimini bulunuz.
| Çözüm: 
|
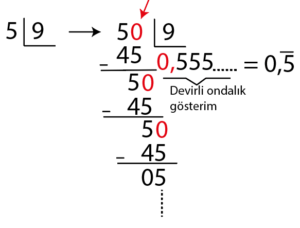
| Örnek: \(\large\frac{5}{9}\) kesrinin ondalık gösterimini bulunuz.
| Çözüm: 
|
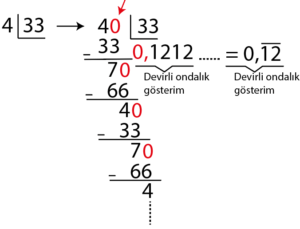
| Örnek: \(\large\frac{4}{33}\) kesrinin ondalık gösterimini bulunuz. | Çözüm: 
|
6.Sınıf Ondalık Gösterimin Bölme İle İlişkisi Konu Anlatımı sonrası aşağıdaki linkleri ziyaret ediniz.
6.Sınıf Matematik Konu Anlatımı için>>
6.Sınıf Matematik Test İndirmek için>>
6.Sınıf Matematik Test Çözmek için>>
6.Sınıf Matematik daha çok döküman için>>